aperture, focal length, plate scale and focal ratio

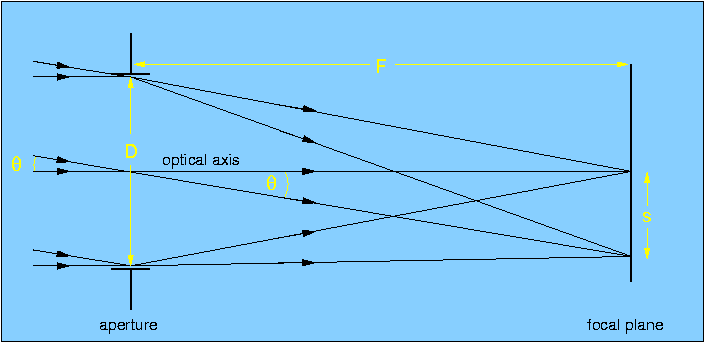
Figure 1 shows the basic function of a telescope. At the left, light from two distant sources arrives at the telescope. As all astronomical sources are effectively at an infinite distance compared to the dimensions of a telescope, the rays from each source can be assumed to be parallel.

The light is collected by an aperture of diameter D which forms an image of the two sources at the focal plane. The line through the centre of the aperture and the focal plane, and orthogonal to them, defines the optical axis of the system. Since the sources are at infinity, the focal length, F, of the telescope is defined by the distance between the focal plane and the aperture. In astronomical telescopes, the aperture is usually a lens or a mirror, and is circular, hence the amount of light collected is proportional to D². The aperture diameter is the single most important parameter affecting the performance of a telescope and hence most telescopes are usually referred to in terms of it, e.g. the ESO 3.6m telescope in Chile, where the 3.6m is the diameter of its primary mirror.

figure 1:

A schematic showing the function of a telescope. The "aperture" in the figure represents an optical element, such as a mirror or lens, with the ability to bring light to a focus.

Two concepts which are extensively used by astronomers when describing the specifications of a telescope are the plate scale and the focal ratio:

• Plate scale, p: This relates the size of the image in the focal plane, s, to its angular size on the sky, . Given that is usually small, figure 1 shows that these two quantities can be related by the equation
  
  s = F ,
  
  where is measured in radians. This equation shows that if an astronomer wishes to study an object of angular size in high spatial detail, s needs to be large, and therefore a long focal-length telescope is required.
  
  Astronomers usually refer to the plate scale in units of arcseconds per mm. As shown in the example problems, the plate scale is then given by
  
  p = 206265 / F,
  
  where F is in mm.
  
  
• Focal ratio, f: This is defined as the ratio of the focal length of the telescope to its diameter, i.e.
  
  f = F / D.
  
  The term is often used in photography, where it refers to the speed of the camera. The larger the focal ratio, the "slower" the camera, as the amount of light falling on a given area of the focal plane is smaller. This can be understood in two ways: for larger F at fixed D, the plate scale is smaller and hence the light is spread out over a larger area; for smaller D at fixed F, less light reaches the given area on the focal plane. For a "faster" camera, the reverse is true.

resolving power

The resolving power (or resolution) of an astronomical telescope is a measure of its ability to distinguish fine detail in an image of a source. Aberrations due to the optical design or flaws in the manufacture and alignment of the optical components can degrade the resolving power, as does peering through the Earth's turbulent atmosphere. We shall come back to address these issues in later lectures. However, even if a telescope is optically perfect and is operated in a vacuum, there is still a fundamental lower limit to the resolving power it can achieve. This is known as the theoretical resolving power, and in this section we shall explore its origins and consequences.

Figure 2 shows a point source at infinity, i.e. a star radiating light into space. Considering the light as a wave, it is possible to define wavefronts, which are points of the wave at equal phase. As the wavefronts propagate from the star at the speed of light, their curvature decreases until they can be considered plane-parallel waves when they arrive at the telescope. A crude analogy would be to consider the waves created when a stone is thrown into the centre of a pond. Close to where the stone entered the water, the wavefronts would be clearly defined circles, whereas by the time they reach the edge of the pond, they would be more or less straight and parallel to the edge of the pond.

figure 2:

Schematic showing wavefronts radiating from a point source at infinity and imaged by a telescope. The "aperture" in the figure represents an optical element, such as a mirror or lens, with the ability to bring light to a focus.

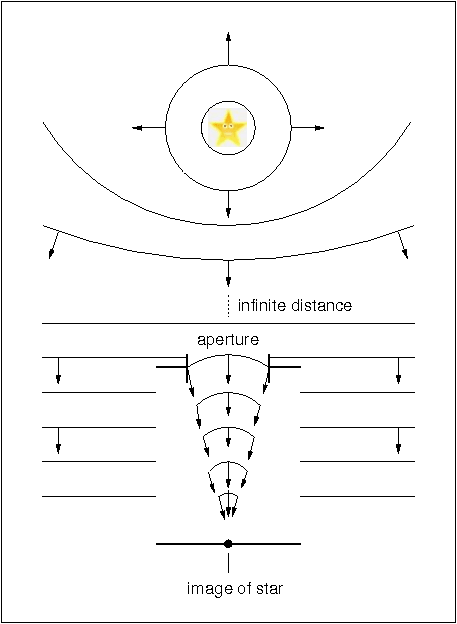
Figure 2 also shows that the telescope brings the plane-parallel waves incident upon the aperture into focus, forming an image of the star in the focal plane. It does this by inducing a phase change on the wavefront which varies across the telescope aperture. However, since the aperture does not cover the entire wavefront radiated by the star, but only a very small portion of it, a diffraction pattern is produced.

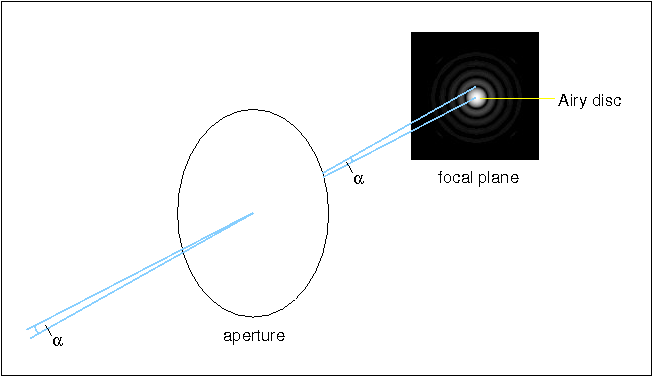
The diffraction pattern produced when imaging a point source with a lens-based telescope is shown in figure 3. The image appears as a spot surrounded by concentric rings which decrease in brightness with increasing distance from the centre. The bright central spot, known as the Airy disc after the British astronomer who first studied it, is theoretically predicted to contain 84% of the light, and the first ring contains less than 2%.

figure 3:

Schematic showing the diffraction pattern produced in the focal plane of a telescope when imaging a point source. is the angle between the centre of the Airy disc and the first minimum and denotes the theoretical resolving power of the telescope.

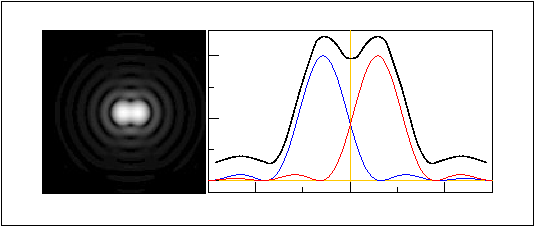
The size of the Airy disc puts a limit on the resolving power of a telescope. According to Rayleigh's criterion for resolution, two point sources are said to be just resolved when the centre of one Airy disc falls on the first minimum of the other diffraction pattern. This results in a 20% drop in intensity between the maxima, as illustrated in figure 4. An expression for Rayleigh's criterion can be obtained from theory by calculating the positions of minima of intensity in a point-source diffraction pattern. For the first minimum, this gives

= 1.22 / D,

where is the wavelength of light and is measured in radians and is the angle subtended at the aperture by the centre of the Airy disc and its first minimum in the focal plane (see figure 3). is commonly referred to as the theoretical resolving power or diffraction-limited resolution of a telescope.

figure 4:

Left: image of the overlapping diffraction patterns from two point sources separated by an angle . Right: The black curve shows a cut through the image on the left. According to Rayleigh's criterion, the two sources are just resolved.

Rayleigh's criterion shows that to increase the resolving power of a telescope it is necessary to observe at shorter wavelengths and/or increase the diameter of the aperture. For small amateur telescopes, Rayleigh's criterion provides a realistic estimate of the resolution obtained, as calculated in the example problems. For large research telescopes, however, the resolution is dominated not by diffraction but by the seeing. We shall return to this topic later.

Having covered the basic principles of telescope optics, we turn now to look at the various different types of telescope design.