Having determined the physical state of stellar material,
we are now in a position to consider the source of stellar energy;
where, of course, we mean the conversion of energy from some other
form in which it is not immediately available to the star to radiate.
How much energy does a star like the Sun need to generate in order to
shine as it does? We know that the luminosity of the Sun is
L = 4 ×
1026 W = 4 × 1026 Js-1.
We have already
noted that fossil and geological records indicate that the properties
of the Sun have not changed significantly for at least 109
years (3 × 1016 s), and hence in that time the Sun must
have lost approximately 1.2 × 1043 J.
Using Einstein's formula for the equivalence of mass and energy,
= 4 ×
1026 W = 4 × 1026 Js-1.
We have already
noted that fossil and geological records indicate that the properties
of the Sun have not changed significantly for at least 109
years (3 × 1016 s), and hence in that time the Sun must
have lost approximately 1.2 × 1043 J.
Using Einstein's formula for the equivalence of mass and energy,
E = mc2,
we find that in this time the Sun must have
converted about 1026 kg of mass into energy and hence its mass will
have decreased by about
10-4 M (i.e. 0.01%).
What can have been the source of this energy? There are four possible
sources which we might consider and we shall address each of them in
turn:
(i.e. 0.01%).
What can have been the source of this energy? There are four possible
sources which we might consider and we shall address each of them in
turn:
- Cooling or contraction
- Chemical reactions
- Nuclear reactions
cooling or contraction
Cooling and contraction are very closely related, so we shall consider
them both together.
Cooling is perhaps the simplest idea of all. Let us suppose that the
energy radiated by the Sun at the present time is simply due to the
fact that the Sun was much hotter when it was formed than it is now
and it has since been cooling down. We can test the plausibility of this
idea by determining how long the present thermal energy content of the
Sun could supply its present rate of energy loss.
Another possibility is that the Sun is slowly contracting with
a consequent release of gravitational potential energy and this
energy is then converted into radiation.
The gravitational energy and the thermal energy of a star can be
related using a very simple equation which we shall now derive.
In an ideal gas, the thermal energy of a particle is obtained by
multiplying kT/2 by the number of degrees of freedom.
As the particles move in three dimensions, we obtain 3kT/2.
The thermal energy per unit volume is then given by
3nkT/2, where n is the number of particles
per unit volume.
Now, we have seen that the
virial theorem can be written:
3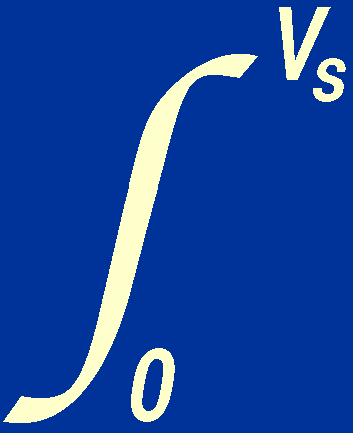 P
dV +
P
dV +  = 0,
= 0,
Assuming that the stellar material is an ideal gas with negligible
radiation pressure, we can substitute the expression
P = nkT in the above equation, to give:
3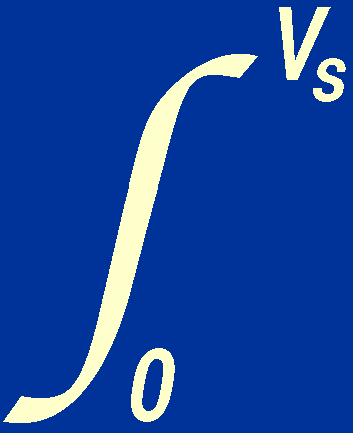 nkT
dV +
nkT
dV +  = 0,
= 0,
Defining the total thermal energy of a star, U, as the
integral over volume of the thermal energy per unit volume,
3nkT/2, we can write:
2U +  = 0.
= 0.
Thus the gravitational potential energy of a star is equal to
twice its thermal energy. This means that the time for which the
present thermal energy of the Sun can supply its radiation and the
time for which the past release of gravitational potential energy
could have supplied its present rate of radiation differ only by a
factor of two, and to get an approximate value for this time we need
consider only one.
Let us consider the gravitational potential energy. We have
seen that
the gravitational potential energy of a star,
 , is given by the inequality:
, is given by the inequality:
-  >
GMs2 /
2rs.
>
GMs2 /
2rs.
We can then approximate a value for the gravitational potential energy
of a star by writing:
-  ~
GMs2 /
rs.
~
GMs2 /
rs.
The total release of
gravitational potential energy would have been sufficient
to provide radiant energy at a rate given by the luminosity of
the star, Ls, for a time:
GMs2 /
Ls rs.
This equation is known as the
thermal
timescale, tth, i.e.:
tth =
GMs2 /
Ls rs.
If we insert values for the mass, radius and luminosity of the Sun in
the above equation we obtain a time of 3 × 107
years. This means that if the Sun were powered by either contraction
or cooling (we can consider either as the factor of 2 is
insignificant), it would have changed substantially in, say, the last ten
million years, a factor of 100 times too short to account for the
constraints on the age of the Sun imposed by fossil and geological
records.
chemical reactions
Perhaps chemical reactions such as the combustion of coal, gas and oil
could supply enough energy to power the Sun? We know that such reactions
release
approximately 5 × 10-10 of the rest mass energy.
But we calculated above that we need to find a process which can release
at least 10-4 of the rest mass energy of the
Sun, so this immediately rules out chemical reactions as the source
of the Sun's energy (which could only power the Sun for a few
thousand years).
nuclear reactions
The only known way in which quantities of energy sufficiently large to
power stars can be produced is through nuclear reactions. There are
two types of nuclear reaction - fission and fusion. Fission
reactions, such as occur in nuclear reactors and the atomic bomb, can
release 5 × 10-4 (i.e. 0.05%) of the rest mass energy
through the splitting (or fission) of heavy nuclei. Fusion reactions,
such as occur in the hydrogen bomb, can release up to 0.01 (i.e. 1%)
of the rest mass energy by combining (or fusing) light nuclei. This
can be proved very simply by considering that the atomic weight of
hydrogen is 1.008172 (defining the weight of O16 as 16) and
that of the isotope He4 is 4.003875. The difference between
the atomic weight of He4 and four times the atomic weight
of hydrogen is 0.0288. This mass difference is transformed into energy
when four protons are fused into one He4 nucleus. The mass
fraction which is transformed into energy in this process is hence
given by 0.0288 / (4 x 1.008172) = 0.007, or 0.7%.
It can be seen that both fusion and fission could in principle power
the Sun. As light elements are much more abundant in the Sun than
heavy ones, one would expect nuclear fusion rather than fission to be
the main source of energy. Given the limits on the pressures and
temperatures of the stars that we have just obtained, however, is it
possible for nuclear fusion to occur in stars? We shall return to
answer this question in detail later in the course.
©Vik Dhillon, 17th October 2013
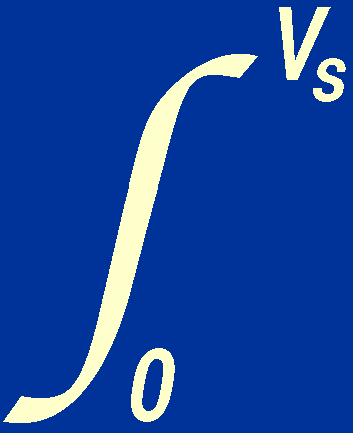 P
dV +
P
dV + 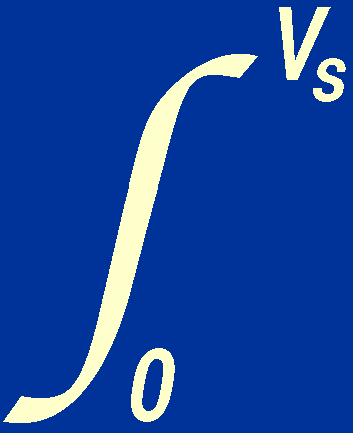 nkT
dV +
nkT
dV +