solving the equations of stellar structure

---

We now have four differential equations which, in the absence of convection, govern the structure of stars:

I
II
III
IV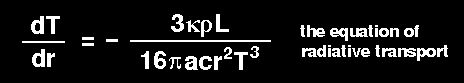

where

r   =	radius
P   =	pressure at r
G   =	gravitational constant
M   =	mass of material within r
=	density at r
L   =	luminosity at r (rate of energy flow across sphere of radius r)
=	energy release per unit mass per unit time
T   =	temperature at r
=	opacity at r
a   =	radiation density constant
c   =	speed of light

These differential equations are supplemented by three additional relations for P, and whose exact form we will consider later in the course. For now, we can say that all of these quantities should depend on the density, temperature and chemical composition of the star (which in turn depend on the radius) and so we can write:

P = P (, T, composition)	the equation of state
= (, T, composition)
= (, T, composition)

Given the chemical composition of the star, we now have seven equations for the seven unknowns P, M, , L, , T and as functions of r. Hence the equations can be solved. Because four differential equations are involved, however, these equations need a set of four boundary conditions before they can be solved. It is obvious that at the centre of a star the mass and the luminosity must go to zero and thus two of the boundary conditions are:

M = L = 0   at   r = 0.

The surface boundary conditions are not so obvious, but simple approximations to them are often used. There is no sharp edge to a star, but the density of the Sun at the visible surface is estimated to be 10^-4 kg m^-3, which is extremely small compared to the value of the mean density of the Sun (1.4 × 10³ kg m^-3) derived earlier. We have also seen that the surface temperature of the Sun (5780 K) is much smaller than its minimum mean temperature (2 × 10⁶ K). Hence, two approximate surface boundary conditions are given by:

= T = 0   at   r = r_s.

The above formulation would in principle enable us to create theoretical models of stars of a given radius. In practice, however, since the radius of a star changes by orders of magnitude during its evolution, it is often more convenient to rewrite the equations of stellar structure in terms of M instead of r. Dividing each of the equations of stellar structure by the equation of mass conservation, we can write:

I.         dP / dM = - GM / 4r⁴,

II.        dr / dM = 1 / 4r²,

III.       dL / dM = ,

IV.       dT / dM = - 3L / 64²acr⁴T³,

where we have also inverted the equation of mass conservation. The corresponding boundary conditions become:

r = L = 0   at   M = 0    and

= T = 0   at   M = M_s.

We can now specify the mass, M_s, and the chemical composition of a star and have a well-defined problem to solve in order to calculate the structure of the star - the differential equations in terms of M, the three subsidiary relations for P, , and the associated boundary conditions. It is possible to solve this problem analytically if certain simplifying assumptions are made, but in general the equations need to be solved numerically on a computer.


modelling the evolution of stars

Until now, we have assumed that the properties of a star do not change with time. Hence the equations of stellar structure we have formulated contain no time derivatives. How then can we study the evolution of stars? Fortunately, in many stages of a star's evolution, the time derivatives are small and can be omitted from the equations. It is then relatively simple to study the slow evolution of a star by assuming that changes in chemical composition are the main factor in determining how the properties of a star changes as it evolves (changes in mass are not so important as most stars lose no more than 1% of their mass during the course of their lives). The structure of the star can first be calculated at a given time. Nuclear reactions then cause a gradual change in its chemical composition and the structure can be recalculated a short time later with the revised chemical composition. This procedure can then be repeated. The process will of course break down if at any time the properties of the star are found to be changing so rapidly with time that time-dependent terms in the equations of stellar structure cannot be regarded as unimportant. In that case the equations must be modified and the problem becomes much more complicated.


modelling convection

We have also assumed in the above formulation of the equations of stellar structure that the effects of convection can be ignored. Most stars, however, contain regions in which a significant amount of energy transport is by convection. How then is it possible to solve for the structure of a star? We can proceed by calculating stellar models without including convection and then, at each point in the star, use the condition for the occurrence of convection derived earlier to determine whether convection is important. If the condition is never satisfied, convection is indeed absent and the structure of the star has been correctly calculated. If the condition is fulfilled at any point, however, convection must be occurring and the whole solution of the equations must be reconsidered, as follows.

Ideally, we would like to know exactly how much energy is transported by convection. The lack of a good theory of convection, however, makes it very difficult to obtain this information. Fortunately, this is not as serious as one might expect. We can obtain an approximate estimate of how much energy can be carried by recalling that heat is convected by rising elements which are hotter than their surroundings and by falling elements which are cooler than their surroundings. If we suppose that each type of element has a temperature which differs by T from its surroundings then, because an element is always in pressure balance with its surroundings, it has an energy content per kg which differs by c_pT from the energy content of a kg of the surrounding medium (where c_p is the specific heat at constant pressure). If we assume the stellar material is a mono-atomic ideal gas, then c_p=5k/2m, where m is the average mass of the particles in the gas. Assuming that a fraction ( 1) of the material is in the rising and falling columns and that they are moving with a speed v ms^-1, then the rate at which excess energy is carried across a sphere of radius r is:

L_conv = surface area of sphere × rate of transport of mass across unit area × excess energy per unit mass.

This can be written as:

L_conv = 4r² . v . 5kT / 2m = 10r²vkT / m.

When discussing the state of stellar material, we derived values of 1.4 × 10³ kg m^-3 and ½(1.67 × 10^-27) kg for the mean density and mean particle mass of the Sun, respectively. With k = 1.38 × 10^-23 J K^-1 and considering the energy crossing a sphere half way between the centre and surface of the Sun (i.e. r = 3.48 × 10⁸ m) we obtain:

L_conv ~ 10²⁶ vT  W.

The surface luminosity of the Sun is L = 3.86 × 10²⁶ W and, as implied in our derivation of the equation of energy production, at no point in the Sun can the luminosity exceed this value. Therefore, provided a reasonable fraction of the material is taking part in the convection, a velocity of a few metres per second and a temperature difference of a few degrees is enough to carry all of the Sun's energy. As the temperature excess and velocity of a rising element is determined by the difference between the actual temperature gradient and the adiabatic gradient, where the latter is defined by

[(P / T) (dT / dP)]_ad = (-1) / ,

this suggests that the actual gradient is not greatly in excess of the adiabatic gradient. To a reasonable degree of accuracy we can assume that the temperature gradient has exactly the adiabatic value in a convective region in the interior of a star and hence we can rewrite the condition for the occurrence of convection in the form:

(P / T) (dT / dP) = (-1) / .

Although we have assumed solar values in the above calculations, the same result is valid in most stars. Thus, in a convective region in a star, the four differential equations

dP / dM = - GM / 4r⁴,

dr / dM = 1 / 4r²,

dL / dM =

(P / T) (dT / dP) = (-1) /

must be solved together with equations for and P. The equation for the luminosity due to radiative energy transport is still true:

L_rad = - (64²acr⁴T³ / 3) (dT / dM),

and once the other equations have been solved L_rad can be calculated. This can then be compared with L calculated from dL / dM = and the difference between the two gives the value of the luminosity due to convective energy transport, i.e. L_conv = L - L_rad. If convection is occurring, L_conv must be positive; if at any time it is found to be negative, this means that radiation is more than capable of carrying all of the energy and hence convection will not occur. In solving the equations of stellar structure, the equations appropriate to a convective region must be switched on whenever the temperature gradient reaches the adiabatic value and these convective equations must then be switched off whenever radiation is capable of carrying all of the energy with a temperature gradient lower than the adiabatic value. It is important to note, however, that this method breaks down near the surface of a star where the density is much lower ( ~ 10^-3 kg m^-3). In order for L_conv to be comparable with the total energy transport of L = 3.86 × 10²⁶ W in this region, the velocity of the rising and falling elements must be comparable with the velocity of sound (~10⁴ ms^-1) and the temperature differences must be comparable with the actual temperature (~10⁴ K). Such velocities and temperature differences can only be driven by a temperature gradient substantially in excess of the adiabatic value and in such a case an expression for the amount of energy carried by convection is required. It is in such low density surface regions that the lack of a good theory of convection is a serious problem.

---

©Vik Dhillon, 27th September 2010