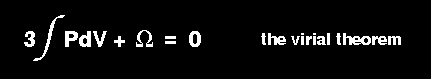One of our immediate aims is to determine the physical state of stellar
material, as a knowledge of this is essential if
we are to understand stellar structure and evolution. Knowing the
minimum central pressure of
a star is not enough. We also need to know the density and temperature
of stellar material. It is a relatively simple matter to determine the
density as we know typical stellar masses and radii.
We can determine the temperature by first formulating an important equation
known as the virial theorem and then using the virial theorem
to calculate the mean temperature of a star.
The virial theorem can be derived as follows. If we divide the
equation of hydrostatic support
by the equation of mass conservation,
we obtain:
(dP / dr) / (dM / dr) =
(- GM  /
r 2) /
4
/
r 2) /
4 r 2
r 2
 .
.
Multiplying both sides of the equation by
4 r 3 and
rearranging gives:
r 3 and
rearranging gives:
4 r 3 dP =
- (GM / r ) dM.
r 3 dP =
- (GM / r ) dM.
If we now integrate this equation over the whole star, we can write:
3 V
dP =
-
V
dP =
- 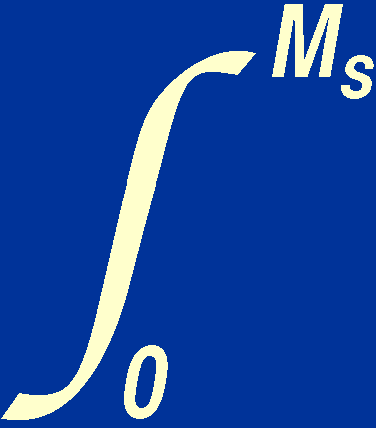 (GM / r)
dM,
(GM / r)
dM,
where V is the volume contained within radius r.
The left-hand side of the above equation can be integrated by parts,
giving:
3 [PV]cs -
3 P
dV =
-
P
dV =
- 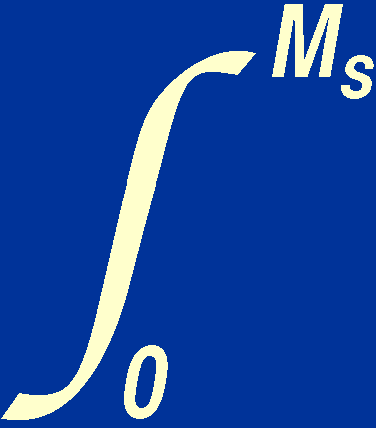 (GM / r)
dM.
(GM / r)
dM.
The volume of the star must increase outwards from zero at the centre of
the star, i.e. Vc = 0, and we assume that there is
a sharp boundary between the surface of the star and the vacuum of space,
i.e. Ps = 0. Hence we may write:
3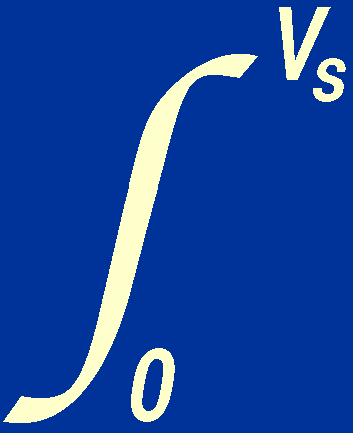 P
dV =
P
dV =
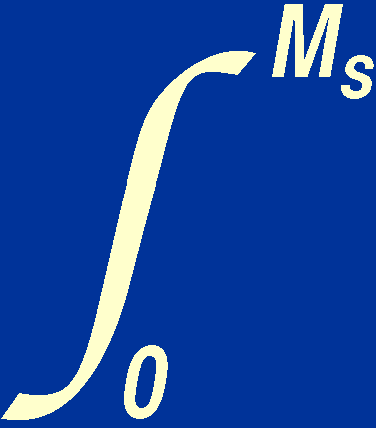 (GM / r)
dM.
(GM / r)
dM.
Now suppose that a mass M has been assembled into a star of
radius r, then the work done ( = force × distance =
mass × acceleration × distance) in bringing an
additional element of mass dM from infinity to r
is:
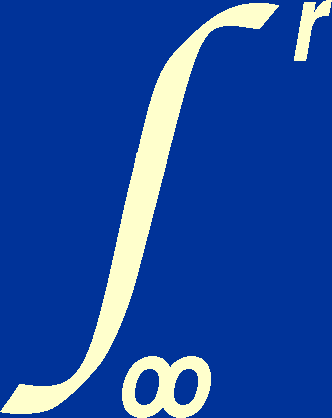 (GM /
r 2) dM dr =
- (GM /
r) dM = d
(GM /
r 2) dM dr =
- (GM /
r) dM = d ,
,
where d is the gravitational potential
energy of the mass element. The gravitational potential
energy of the star is then the integral over M of the above
equation,
is the gravitational potential
energy of the mass element. The gravitational potential
energy of the star is then the integral over M of the above
equation,
 =
-
=
- 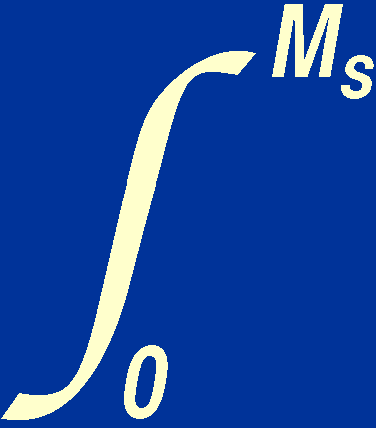 (GM /
r) dM.
(GM /
r) dM.
Note that the minus sign here is a matter of convention, where the
zero of gravitational potential energy is chosen to be at infinite
distance. We could instead have chosen to integrate from r to
infinity, in which case the minus sign would disappear. The key point
is that the above form of the equation gives the work done,
i.e. the energy required, to form the star from its constituent
parts. Since assembling a star from its constituent parts at infinity
does not require any work to be done, but instead releases energy, the
above equation is negative. Had we swapped the integration limits and
hence removed the minus sign, the equation would tell us the energy
required to disperse a star to infinity, which would clearly require
positive work to be done against gravity.
Hence we can write:
3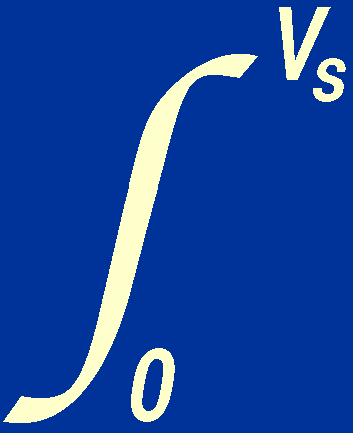 P
dV +
P
dV +  = 0.
= 0.
This equation, which is of great importance in astrophysics, is known as
the virial theorem and, as we shall see when discussing
energy generation, it relates the
gravitational energy of a star to its
thermal energy.
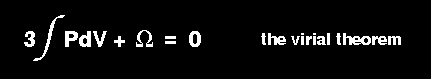
©Vik Dhillon, 27th September 2010
 V
dP =
-
V
dP =
- 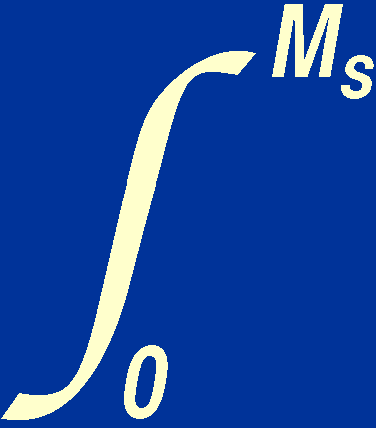 (GM / r)
dM,
(GM / r)
dM, P
dV =
-
P
dV =
- 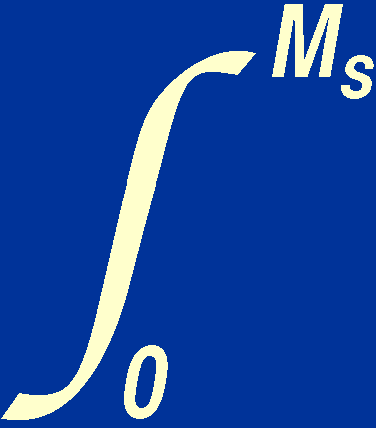 (GM / r)
dM.
(GM / r)
dM.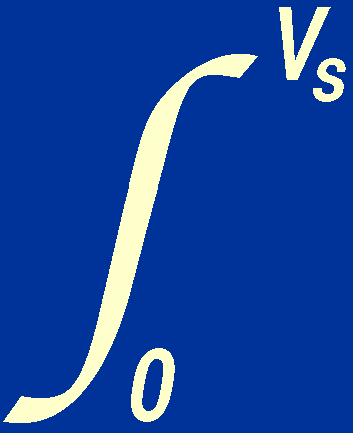 P
dV =
P
dV =
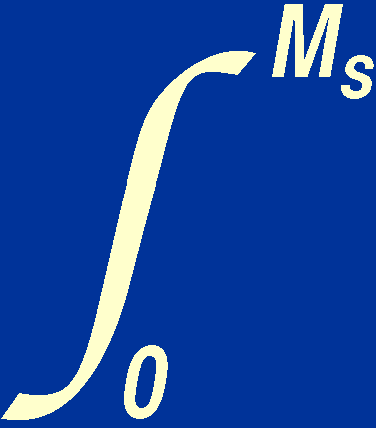 (GM / r)
dM.
(GM / r)
dM.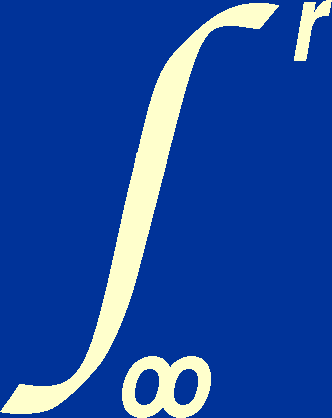 (GM /
r 2) dM dr =
- (GM /
r) dM = d
(GM /
r 2) dM dr =
- (GM /
r) dM = d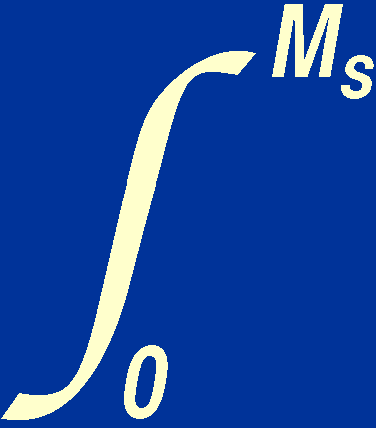 (GM /
r) dM.
(GM /
r) dM.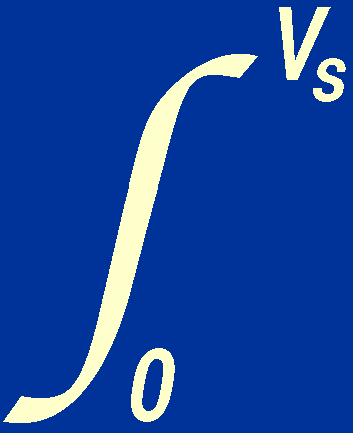 P
dV +
P
dV +