We set out to create a simulation of the balloon's flight, so that we could predict a number of unknown parameters.
By knowing the expected mass of our payload, we could use the simulation to determine the size of the balloon
and parachute needed to launch and safely return the payload, as well as the amount of helium required to achieve
the desired height and ascent velocity.

To do this, we first created a simple model of the atmosphere (based around the U.S. standard atmosphere 1976 model).
This allowed us to build a pressure, atmospheric density and temperature profile for the atmosphere. This can
be seen in figure 1. Then, using simple Newtonian mechanics and the following equations, P_z=P_oexp(-mgz/kT), T_z=T_o+Lz
and F_drag=0.5ρV²AC_d we were able to predict the rate of ascent and descent of the balloon, as well as the rate of the
balloon's expanding radius. This can be seen in figure 2. Together, this allowed us to estimate the maximum altitude that
our balloon reaches (this is where the balloon will burst) and the total flight duration.

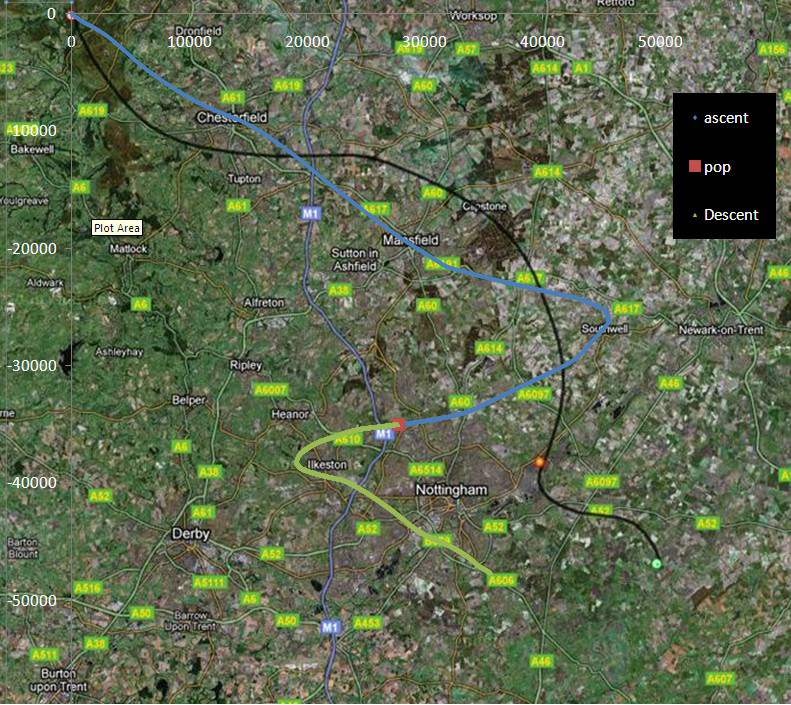
It is also possible to predict approximately where the payload and parachute will land. Wind data for different altitudes
can be obtained from the nomads.ncdc.noaa.gov website (full details on how to do this the low-tech but time consuming way
will be provided on this page soon). By correlating this data with the ascent and descent data, the second-by-second position
of the payload can be calculated. This is done with the assumption that the payload will always be travelling approximately
at the same speed as the wind and using the equation d_new=d_old+v_wind. Figure 3 shows one of our early attempts
compared with results from the CUSF online predictor.

Figure 1



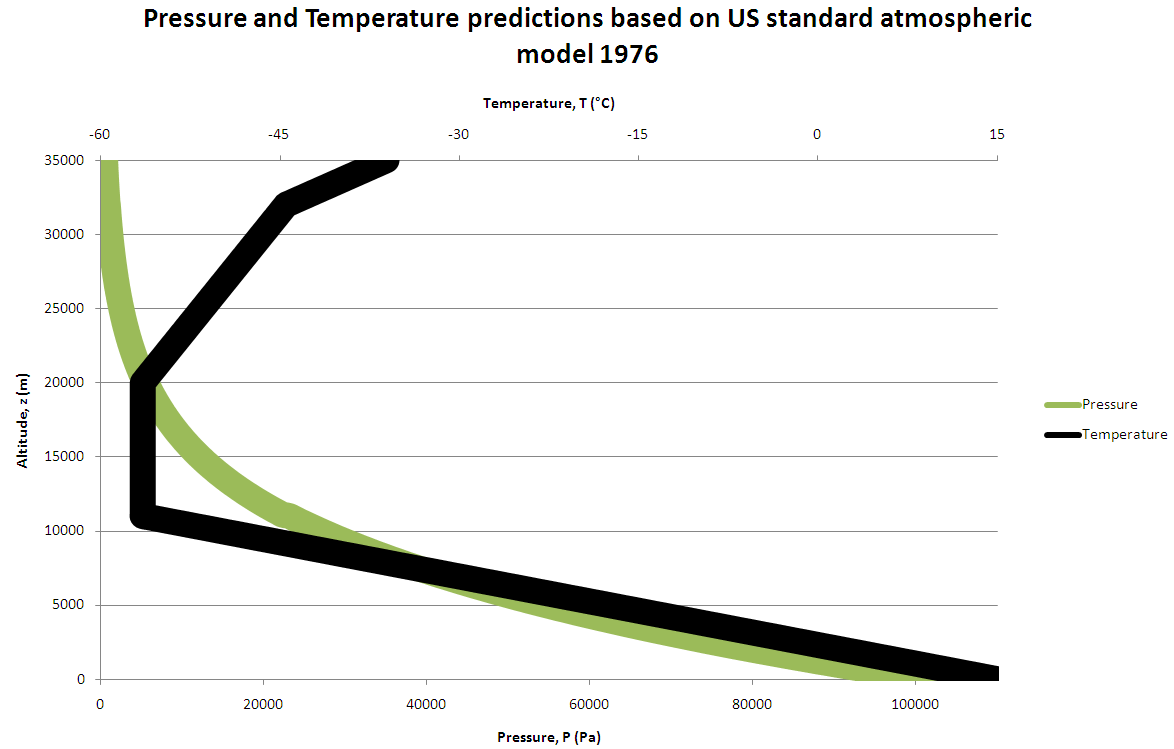
Figure 2



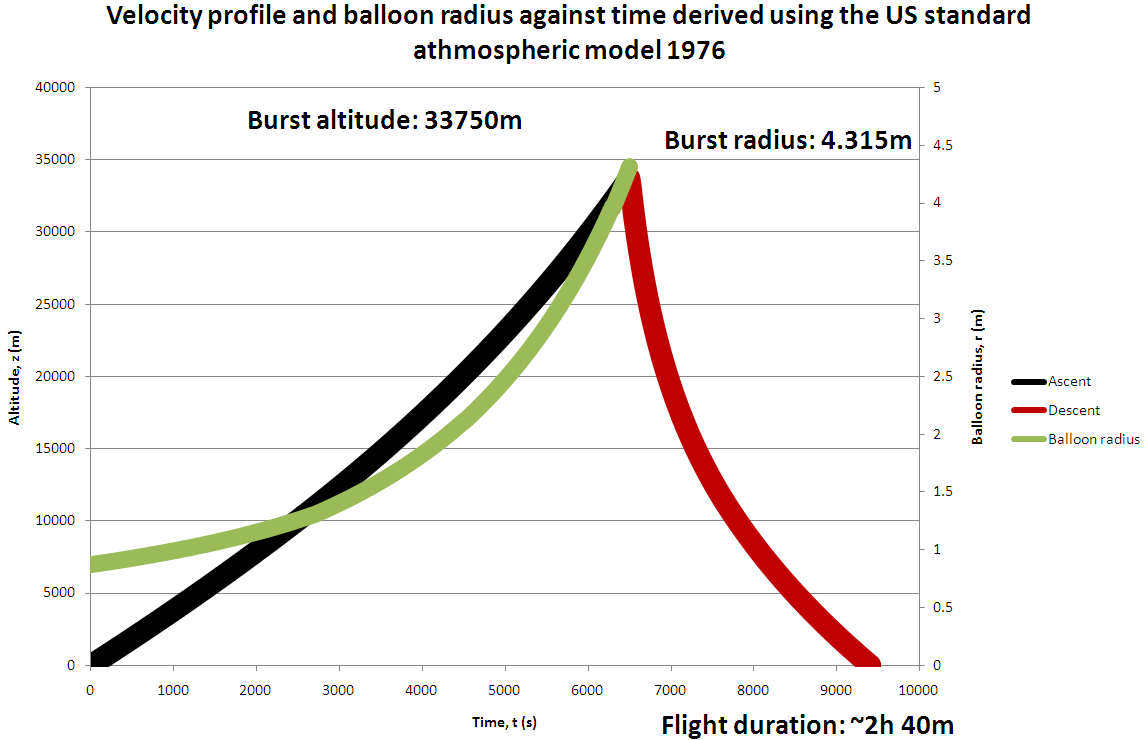
Figure 3