vik dhillon: phy213 - the physics of stellar interiors

approximate form for opacity

Our aim is to derive an expression for the opacity which can be used to solve the equations of stellar structure. Hence the opacity should have the form:

(, T, chemical composition).

A discussion of the detailed form for opacity is outside the scope of this course - it involves complicated numerical calculations in atomic physics. In restricted ranges of density and temperature, however, the results of detailed calculations can be represented by simple power laws of the form

₀ T,

where

and are slowly varying functions of density and temperature and

₀ is a constant for stars of a given chemical composition. Figure 13 shows how the power law approximations fit the curve derived from detailed opacity calculations.

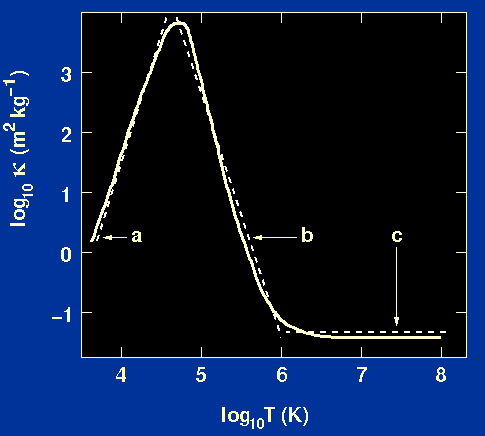
Figure 13:

The solid curve shows opacity as a function of temperature for a star of given density (10^-1 kg m^-3) and chemical composition. The dotted lines are the approximate power-law forms for the opacity described below.

Figure 13 shows that the opacity is low at high temperatures and remains constant with increasing temperature. This is because at high temperatures most of the atoms are fully ionised and the photons have high energy and are free-free absorbed less easily than lower energy photons. In this regime the dominant opacity mechanism is hence electron scattering, which is independent of T, resulting in an approximate analytical form for the opacity given by

= = 0, i.e.

₀ (curve c in figure 13).

Figure 13 shows that the opacity is also low at low temperatures and decreases with decreasing temperature. In this regime, most atoms are not ionised and there are few electrons available to scatter radiation or to take part in free-free absorption processes, while most photons have insufficient energy to ionise atoms via free-bound absorption. An approximate analytical form for the opacity at low temperatures is given by

= ½ and = 4, i.e.

₀ ^½ T⁴ (curve a in figure 13).

Figure 13 shows that the opacity has a maximum at intermediate temperatures where bound-free and free-free absorption are very important and thereafter decreases with increasing temperature. A reasonable analytical approximation to the opacity in this regime is given by

= 1 and = -3.5, i.e.

₀ / T^3.5. (curve b in figure 13).

In the next part of the course we will see how it is possible to use these simple approximate expressions for the opacity in conjunction with the equations of stellar structure to obtain some important insights into the structure of stars.