| solving the lane-emden equation |
|
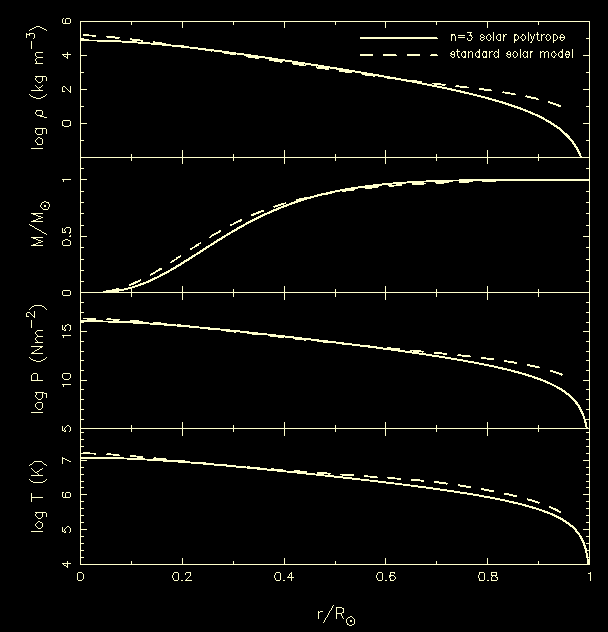
| Figure 22: |
Numerical solutions to the Lane-Emden equation for (left-to-right)
n = 0, 1, 2, 3, 4 and 5.
|
| Table 2: |
Numerical solutions to the Lane-Emden equation, showing the
polytropic index n and the values of
|
|
n |
|
- |
| 0 | 2.45 |
3.33 x 10-1 x |
| 1 | 3.14 |
1.01 x 10-1 x |
| 2 | 4.35 |
2.92 x 10-2 x |
| 3 | 6.90 |
6.14 x 10-3 x |
| 4 | 15.00 |
5.33 x 10-4 x |
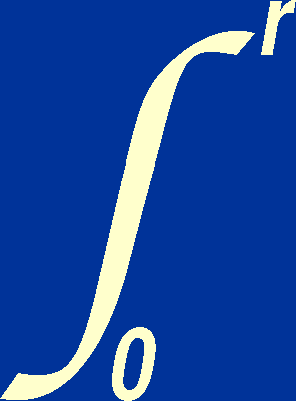 4
4 

| Figure 23: |
Comparison of numerical solution for an n = 3 polytrope of the
Sun versus the Standard Solar Model.
|