vik dhillon: phy213 - the structure of main-sequence stars

detailed stellar models

Using homologous stellar models, we were able to determine the slopes of the main-sequence in the HR diagram and the mass-luminosity relation to a reasonable degree of accuracy. Using polytropes, we were able to model the interior structure of stars to a reasonable degree of accuracy without knowing anything about how the energy is produced and transported within stars. To proceed further, and so arrive at a more accurate model of the structure of a star, we need to integrate the full set of 7 equations of stellar structure using a computer. When this is done, the effective temperatures and luminosities at the surfaces of the stellar models are found to increase with total mass in a way that satisfactorily reproduces the observed HR diagram and mass-luminosity relation (see figures 49 and 50 of Tayler), giving confidence that the theory of stellar structure is correct. As well as correctly predicting the surface values of quantities such as luminosity and effective temperature, detailed stellar models also predict the way in which these and other quantities vary in the interior of a star. Such a model of the internal structure of the Sun is shown in figure 21.

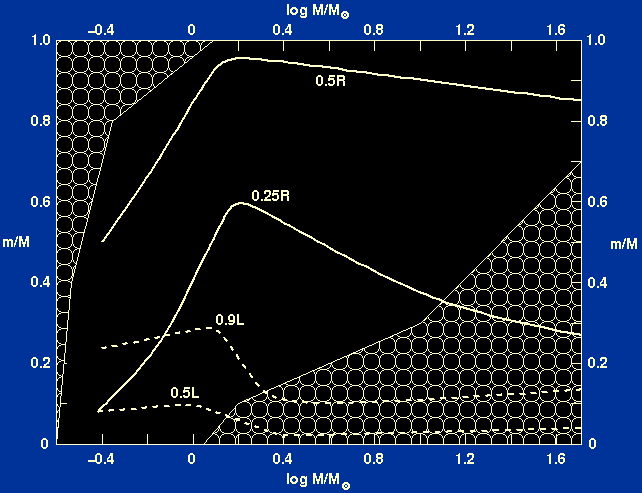
Figure 21:

The variation of mass, luminosity, temperature, density and pressure with radius in a model of the Sun. The mass, luminosity and radius are given in terms of their surface values, and the temperature, pressure and density in terms of their central values.

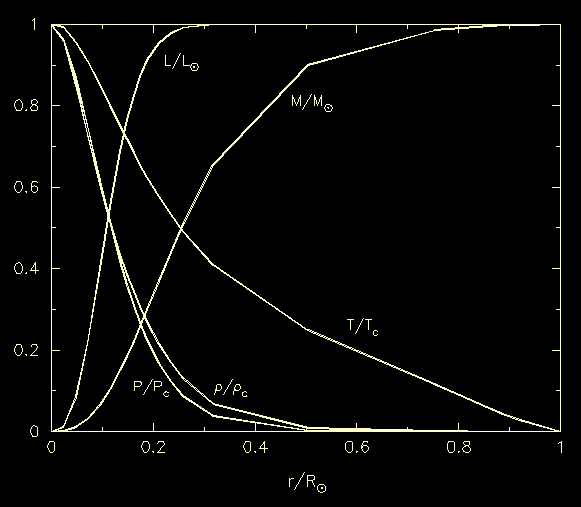
The density (and pressure) in the Sun drops to about 0.1% of its central value at about 0.5R. This is a characteristic of most stars, in which the mass is concentrated towards the centre; for the Sun, 90% of the mass is within 0.5R (0.125 of the volume). The energy generation (i.e. luminosity) is even more concentrated in radius, with 99% being within 0.25R.

Figure 22 shows the distribution of element abundances in the interior of the Sun, calculated by assuming an originally homogeneous Sun with 27% helium, 71% hydrogen and 2% heavy elements by mass and then burning hydrogen to helium according to local temperatures and densities.

Figure 22:

The distributions of hydrogen, helium, carbon and nitrogen in a model of the Sun.

The proton-proton chain is the dominant source of energy in stars with masses less than about 1.1M. The proton-proton chain is not very sensitive to temperature and hence some hydrogen is able to burn in off-core regions. This can be seen in figure 22, which shows that there is some change in hydrogen abundance out to 0.25R. Figure 22 also shows that there is a change in the carbon and nitrogen abundances in the central regions, where the CNO cycle is operating very slowly. Since this has been going on for the lifetime of the Sun, which is significantly longer than the rate of the slowest reaction in the CNO cycle, there has been enough time to achieve equilibrium abundances of ¹²C and ¹⁴N. Nitrogen is therefore enriched by a factor of 7 while carbon is depleted by a factor of 200, resulting in nitrogen being 300 times as abundant as carbon in the core.

So far we have only looked at the interior of a model of the Sun. What about the internal structure of stars of different masses? As demonstrated during our discussion of homologous stellar models, the way in which any physical quantity such as luminosity varies from the centre of a main-sequence star to its surface can be assumed to be (very) approximately the same for all stars, regardless of mass, and only the absolute values vary from star to star. However, there is one way in which detailed models of the interiors of stars of different masses do significantly differ from each other - the position and extent of the convectively unstable regions. We have already seen that the condition for the occurrence of convection can be satisfied in two ways; either the ratio of specific heats is close to unity or the temperature gradient is very steep. The former occurs in cool layers, where the gas is partially ionized, while the latter occurs in very hot layers where the energy generation rate is high. Where, or whether, such layers occur in a particular star depends on the mass of the star, as shown in figure 23.

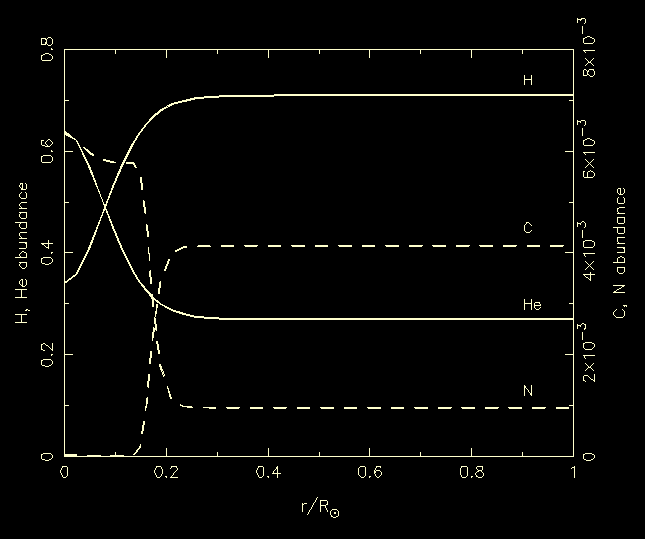
Figure 23:

The extent of the convective regions inside stars is shown as a function of stellar mass. A vertical line in the diagram represents the mass distribution inside a star of that mass. `Cloudy' areas indicate convective regions. The solid lines show the mass values for which the radius is 0.25 and 0.5 of the total radius; the dashed lines show the masses within which 0.5 and 0.9 of the luminosity is produced.

In stars with masses below about 1.3M, the surface layers are cool enough to be partially ionised and they are hence unstable to convection. The structure of solar-type stars then consists of a hot radiative core, at the centre of which the nuclear energy is produced, surrounded by a cool convective envelope. The envelope is shallow for stars near the upper-mass limit but becomes gradually deeper for lower-mass stars, and stars with masses less than about 0.3M are believed to be fully convective. In stars with masses greater than about 1.1M, the central temperature is high enough for the CNO cycle to dominate. The CNO cycle is much more sensitive to temperature than the proton-proton chain, resulting in a steeper temperature gradient which is unstable to convection. Stars considerably more massive than the Sun therefore have a convective core, which contains the energy-generating regions, and a radiative envelope. Stars just a little more massive than the Sun may have both a small convective core and a shallow convective envelope. The mass in the convective core increases with the total mass of the star and very massive stars, like very low-mass stars, may be fully convective.

The structure of main-sequence stars is now believed to be fairly well understood, apart from the uncertainties in the theory of convection. A star will spend some 90% of its life on the main sequence, burning hydrogen to helium at its centre. Eventually, all of the hydrogen is used up in the core, and the star begins to evolve off the main sequence. The last 10% of a star's life is much more eventful than the main-sequence stage, as we shall now see.