| example problems |
|
| 1. |
The latitude and longitude of Sheffield
are 53°23´12´´ N
and 1°28´07´´ W, respectively.
The latitude and longitude of Sydney are
33°55´24´´ S and 151°17´03´´ E,
respectively. What is the difference in the latitude of the two cities in decimal degrees? Difference in latitude = 53°23´12´´ - ( - 33°55´24´´) = 87°18´36´´ Difference in latitude = 87° + (18/60)° + (36/3600)° = 87.3100° What is the difference in the longitude of the two cities in decimal degrees? Difference in longitude = 1°28´07´´ - ( - 151°17´03´´) = 152°45´10´´ Difference in longitude = 152° + (45/60)° + (10/3600)° = 152.7528° What is the difference in longitude in hours, minutes and seconds of time? Difference in longitude = 24 x 152.7528 / 360 = 10.18352h Difference in longitude = 10h (0.18352 x 60)m = 10h11.0112m Difference in longitude = 10h11m (0.0112 x 60)s = 10h11m00.67s What are the co-latitudes of Sheffield and Sydney? Latitude of north pole = 90° N co-latitude of Sheffield = 90° - 53°23´12´´ = 36°36´48´´ Latitude of south pole = 90° S co-latitude of Sydney = 90° - 33°55´24´´ = 56°4´36´´ |
| 2. |
Given that the mean radius of the Earth is
6370 km, convert the nautical mile and the
knot into miles
and mph. Circumference of the Earth = 2 Number of arcminutes in 360° = 360 x 60 = 21600´ Length of arc subtended by 1´ = 2 Therefore, 1 nautical mile = 1.85 km = 1.85/1.61 miles = 1.15 miles and, 1 knot = 1.85 km/h = 1.15 mph. |
| 3. |
How much longer will it take to fly from Sheffield to
Petropavlovsk in Russia along the parallel
compared to the great circle route?
Assume that Sheffield
and Petropavlovsk are at the same latitude (53°23´ N), the
longitude of Sheffield and Petropavlovsk are 1°28´ W
and 158°42´ E, respectively,
and the plane is flying at 500 knots.
|
|
figure 8: |
a flight from Sheffield to Petropavlovsk in Russia |
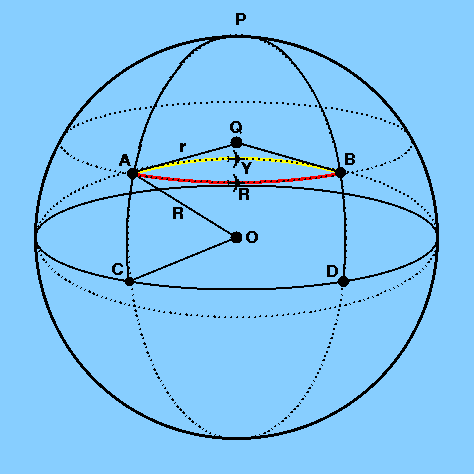
Let A and B in Figure 8 represent Sheffield and Petropavlovsk,
so that
the parallel route is denoted by the red arc ARB and the great circle
route is denoted by the yellow arc AYB. If the
meridians
PAC and PBD are drawn from the north pole P
through A and B to the equator CD, triangle
PAYB is a
spherical triangle.
Applying the cosine formula, we
may then write
cos AYB = cos AP cos BP + sin AP sin BP cos APB
AP = BP = 90° - 53°23´ = 36°37´ = 36.6167°
APB = 1°28´ - (- 158°42´) = 160°10´ = 160.1667°.
Substituting these numbers into the cosine formula gives
cos AYB = (cos 36°.6167)2 + (sin 36°.6167)2 cos 160.1667°
AYB = 71°.9663 = 71°58´ = 4318´.
The great circle distance between Sheffield and Petropavlovsk is
therefore 4318 nautical miles and hence it will take 4318/500 = 8.636 h =
8h38m to complete the journey via the yellow arc in
Figure 8.
The distance between Sheffield and Petropavlovsk along
the parallel of latitude
53° 23´ N
(a measurement often referred to as
the departure)
can be calculated as follows:
The circumference of the parallel at latitude 53°23´ N = 2 ![]() r,
r,
where r = R cos AOC, AOC = 53°23´ =
53.3833° and R = radius of the Earth = 3443 nautical
miles.
The red arc ARB in Figure 8
covers only a fraction of this
circumference, where the fraction is given by AQB/360°
and AQB is given by the difference in longitude
of A and B. So,
ARB = (160°.1667/360°) x 2 ![]() x 3443 x cos 53°.3833 = 5741 nautical miles.
x 3443 x cos 53°.3833 = 5741 nautical miles.
Hence it will take 5741/500 = 11.482 h =
11h29m to complete the journey via the red arc in
Figure 8 and so the journey between Sheffield and
Petropavlovsk is 2h51m quicker along the great circle
route than along the parallel.