| equation of state of a degenerate gas |
|
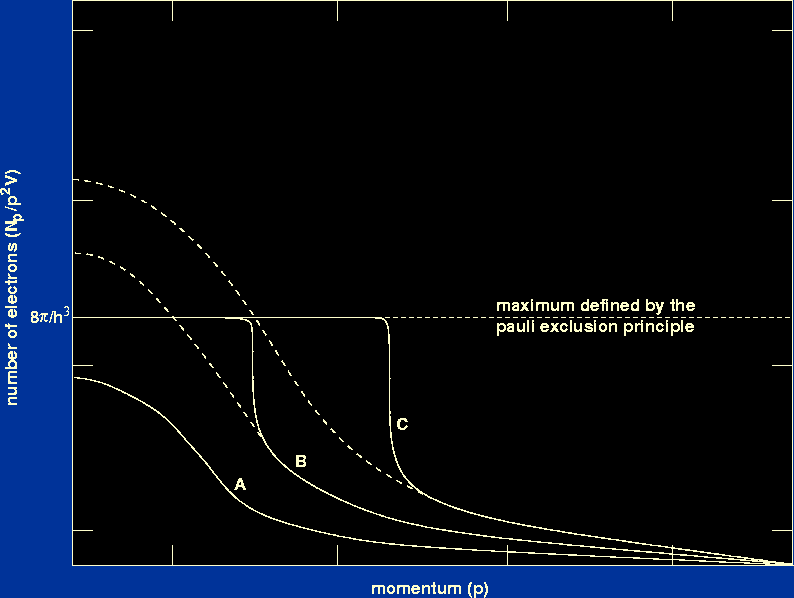
| Figure 11: |
The effect of the Pauli exclusion principle on the Maxwellian
distribution of electron momenta.
|
|
p |
Np =
8 |
| p > p0, | Np = 0. |
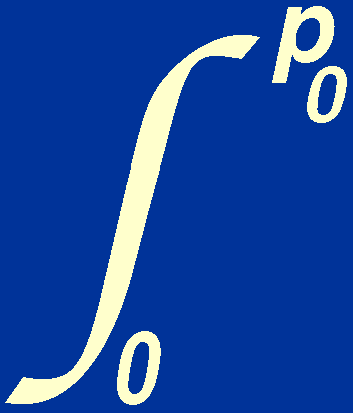 p2
dp =
8
p2
dp =
8 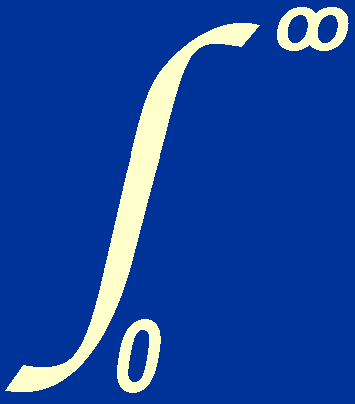 (Np / V ) pvp dp,
(Np / V ) pvp dp,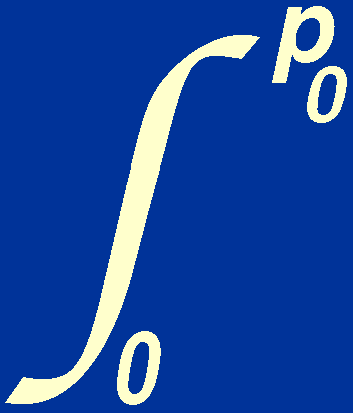 p4 dp /
(1 +
p2 /
me2c2)1/2.
p4 dp /
(1 +
p2 /
me2c2)1/2.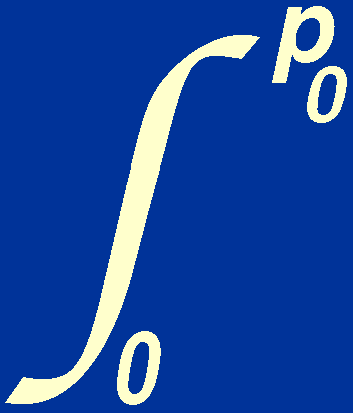 p4 dp =
8
p4 dp =
8 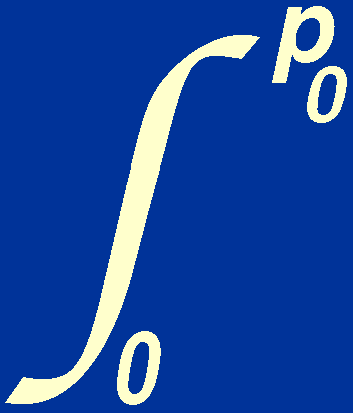 p3 dp =
8
p3 dp =
8 |
Pgas = K1 |
equation of state of a non-relativistically degenerate gas |
|
Pgas = K2 |
equation of state of a relativistically degenerate gas |