vik dhillon: phy105 - the celestial sphere

solar time

Ordinary daily activities are so linked with the Sun's position in the sky that it is natural that civil timekeeping is based on the hour angle of the Sun (HAS) instead of the hour angle of the first point of Aries. This is known as apparent solar time (AST):

AST = HAS

and is zero when the Sun crosses the observer's meridian.

An apparent solar day is defined as the time interval between successive passages of the Sun across the observer's meridian. The time it takes the Sun to return to the same point in the sky each day is slightly longer than one sidereal day, which is the time it takes the stars to return to the same point in the sky each night. This is illustrated in Figure 20.

figure 20:

Solar and sidereal time.

An observer at O₁ on the surface of the Earth observes the Sun and a star on the meridian. Taking the distance of the star to be effectively infinite compared to the Sun, the observer will next observe the star to transit at O₂ when the Earth has rotated once on its axis. However, in the time the Earth has taken to rotate once on its axis, it has also moved in its orbit around the Sun by 360/365.25=0.99°, from position E₁ to E₂. The Earth will thus have to rotate on its axis until the observer is at O₃ for the Sun to appear again on the meridian. The apparent solar day is therefore longer than the sidereal day by a time interval equal to the time it takes the Earth to rotate on its axis by the angle 360°/365.25, i.e. approximately 4 minutes. Given that an apparent solar day is 24 solar hours in length, this means that a sidereal day is only 23^h56^m long in solar units and represents the rotation period of the Earth. Another way of expressing this is that the Sun appears to move backwards amongst the stars by 4 minutes (or 1°) each day.

Each type of day (apparent, solar and sidereal) can be divided into hours, minutes and seconds, but the solar version of each is 24^h/23^h56^m = 1.0028 times or 0.28% longer than the sidereal equivalent.

A sidereal day has a constant length, apart from small fluctuations in the Earth's rotation rate. However, because the Earth's orbit around the Sun is an ellipse, the Earth's orbital speed varies during the year, causing an apparent solar day to vary in length, i.e. the rate of motion of the Sun on the ecliptic is not uniform. For this reason, and also because the ecliptic is inclined to the celestial equator (along which the Sun's hour angle is measured), the rate of change of the hour angle of the Sun varies from day to day. Hence the apparent solar time, which is the time measured by a sundial, is not convenient for most modern purposes because of its variability. Instead, astronomers use mean solar time (MST), which is measured in terms of a fictitious body called the mean sun that moves along the celestial equator with a uniform motion in right ascension equal to the mean motion of the real Sun (about 4 minutes of right ascension per day). The time between successive passages of the mean Sun over the observer's meridian is then constant. This time interval is called a mean solar day. If the hour angle of the mean sun is HAMS, we can write:

MST = HAMS +/- 12^h.

The 12^h correction is put in to make the mean solar time 0^h at mean midnight rather than at mean noon when the Sun crosses the meridian. The plus sign is used when the HAMS lies between 0^h and 12^h and the minus sign when the HAMS lies between 12^h and 24^h.

To define the relationship between the positions of the real Sun and the mean sun we have to consider the concept in more detail. The situation is depicted in Figure 21. The problem is to obtain a body related to the real Sun, S, but which moves so that its right ascension increases at a constant rate. It is solved in two stages:

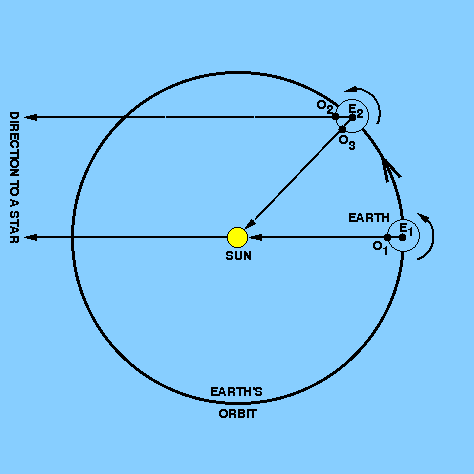
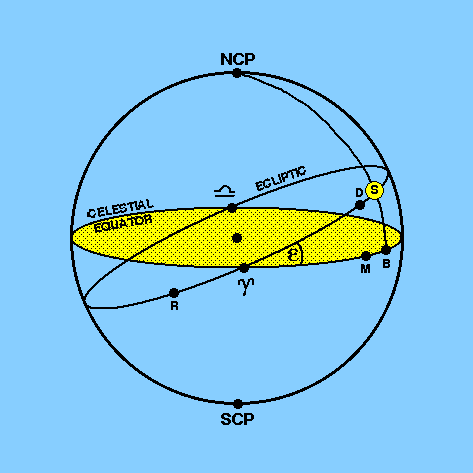
The Sun is said to be at perigee, R, when it is nearest to the Earth. This occurs once per year around January 1st. A fictitious body called the dynamical mean sun, D, is introduced which starts off from perigee with the Sun, moves along the ecliptic with the mean angular velocity of the Sun and consequently returns to perigee at the same time as the Sun.

2.	When this dynamical mean sun, moving in the ecliptic, reaches the first point of Aries, , the mean sun, M, starts off along the celestial equator with the Sun's mean angular velocity, returning to at the same time as the dynamical mean sun.

figure 21:

The positions of the Sun, the mean sun, the dynamical mean sun and the perigee on the celestial sphere.

The meridian from the north celestial pole (NCP) through the Sun meets the celestial equator at B so that the arc

B is the Sun's right ascension (RAS). The right ascension of the mean sun, RAMS, is the arc

M. The quantity BM is referred to as the equation of time, E, and is defined by the relation:

E = RAMS - RAS.

The equation of time varies from a value of about -14.25^m to about +16.25^m throughout the year as the mean sun and the Sun get ahead of each other, as shown in Figure 22.

figure 22:

The annual variation of the equation of time.

Many sundials carry a table of values of the equation of time at various dates throughout the year, enabling the observer to deduce mean solar time from the apparent solar time given by the sundial. An example is shown in Figure 23.

figure 23:

A photograph of an equatorial sundial, clearly showing the shadow cast by the gnomon. The equation of time is marked on the stone slab at the foot of the sundial.

Given the relation LST = RAX + HAX we derived earlier, we can write

LST = RAS + HAS = RAMS + HAMS

and hence

E = HAS - HAMS.

The equation of time is therefore equal to the difference in hour angle between the real Sun and the mean sun.