vik dhillon: phy105 - celestial mechanics - ptolemy, copernicus and galileo

ptolemy, copernicus and galileo

The stars are sufficiently distant that, to the naked eye, they appear to be fixed to the celestial sphere. This is not true of the planets. Ancient astronomers observed that the planets not only wandered on the celestial sphere (like the Sun), but occasionally appeared to stop and retrace their steps for a while, sometimes moving in a great loop, before advancing once again. These planetary phenomena fascinated and frustrated the ancient astronomers. In this series of lectures we will describe the historical efforts to explain these motions - efforts which culminated in the creation of celestial mechanics, a branch of astronomy devoted to the study of the orbits of celestial bodies, such as the planets, satellites, comets, asteroids and spacecraft.

In the 2nd century A.D., Ptolemy wrote the Almagest. This great astronomical work dominated astronomical thought right up to the early years of the seventeenth century. The Ptolemaic Universe is an Earth-centred, or geocentric, one and is depicted in Figure 26. The Sun and Moon revolve about the Earth and the stars are fixed to the surface of a transparent sphere which rotates westwards with a period of one sidereal day. Mercury and Venus move in circles, called epicycles, whose centres are fixed on the line joining the Sun to the Earth. The rest of the planets also move in epicycles, whose centres themselves move in large circles centred on the Earth.

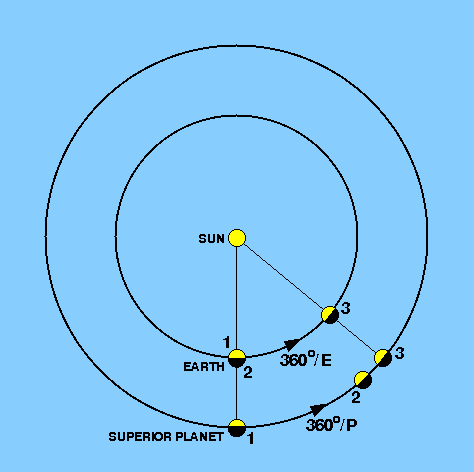
figure 26:

The Ptolemaic Universe.

The Ptolemaic model was remarkably successful in accounting for the known phenomena of the celestial sphere. It was only in the Middle Ages, when Arabian astronomers had accumulated more accurate observations of the planets, that the validity of the Ptolemaic model began to be questioned. Only by further complicating the model by adding epicycles to epicycles and by tilting the orbits was it possible to explain the latest data.

This led Nicolaus Copernicus in the sixteenth century to formulate a completely new and much simpler theory of the Universe in which the Sun is at the centre of the Universe. In this heliocentric Universe, the motions of the planets are accounted for by supposing that they revolve about the Sun in circular orbits but with their centres slightly displaced from that of the Sun. Copernicus also had to keep a few small epicycles. The Moon revolves about the Earth, as in the Ptolemaic Universe, but the Earth rotates on its axis, thereby accounting for the rotation of the stars on the celestial sphere. For a nice animation comparing the geocentric and heliocentric world views, click here.

Copernicus placed the planets at different distances from the Sun. The planets closer to the Sun than the Earth are called inferior planets; these are Mercury and Venus. The planets orbiting farther from the Sun than the Earth are called superior planets; these are Mars, Jupiter and Saturn (Uranus and Neptune were not discovered until later). The motions of the inferior planets as seen in the night sky differ markedly from the motions of the superior planets. The reason for this can be seen from Figure 27. We define:

elongation - the angle seen at the Earth between the direction to the Sun and the direction to a planet. A planet can be at an eastern elongation or a western elongation, depending on whether the planet lies to the east or west of the Sun as seen from the Earth. The elongation of a superior planet can vary from 0° to 180°. Inferior planets, on the other hand, attain a greatest elongation (28° for Mercury and 48° for Venus).
conjunction - an elongation of 0°. An inferior conjunction occurs when the planet lies between the Earth and the Sun. A superior conjunction occurs when the planet lies on the opposite side of the Sun to the Earth. Only inferior planets can be at inferior conjunction.
quadrature - an elongation of 90°. A planet can be at either eastern quadrature or western quadrature, depending on whether the planet lies to the east or the west of the Sun when viewed from the Earth. Inferior planets can never be at quadrature.
opposition - an elongation of 180°. At opposition, a planet lies on the observer's meridian at apparent midnight. Inferior planets can never be in opposition.

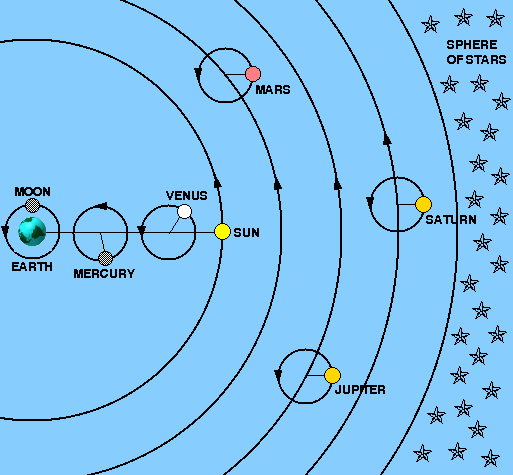
figure 27:

Planetary configurations in the Copernican model. The view is looking down from the north pole of the ecliptic.

It is not only the motions of the inferior and superior planets which differ markedly when viewed from the Earth. The variety of phases exhibited by superior planets differ markedly from those of the inferior planets. This is due to the fact that the planets all shine by reflected sunlight and so half of a planet is always sunlit while the other half is dark. The fraction of the sunlit hemisphere seen from the Earth, however, varies with the planetary configuration, as shown in Figure 27. The phase termed new occurs when we see only the dark hemisphere. This can only occur at inferior conjunction and so can never be seen on the superior planets. Full phase, when the entire sunlit hemisphere of a planet is visible from the Earth, occurs when a planet is in opposition and so can only ever be observed on a superior planet (the inferior planets at superior conjunction also show a full phase, but this is lost in the glare of the Sun). The superior planets can never be observed in crescent phase, when less than half of the observable hemisphere is sunlit, whereas inferior planets can. Superior planets are almost always observed in gibbous phase, when more than half of the planet appears sunlit. Inferior planets also exhibit gibbous phases.

Copernicus correctly stated that the farther a planet lies from the Sun, the slower it moves around the Sun. When the Earth and another planet pass each other on the same side of the Sun, the planet appears to retrace its path for a short while (which is known as retrograde motion) and then continue in its original direction (which is known as prograde motion). Figure 28 shows why this occurs: as we view the planet from the moving Earth, our line of sight reverses the apparent motion of the planet twice. When the orbits of the Earth and the planet are not co-planar, the motion of the planet in the sky appears as a loop.

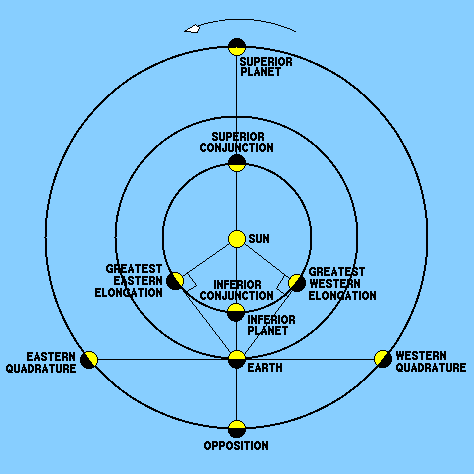
figure 28:

Retrograde motion in the Copernican model.

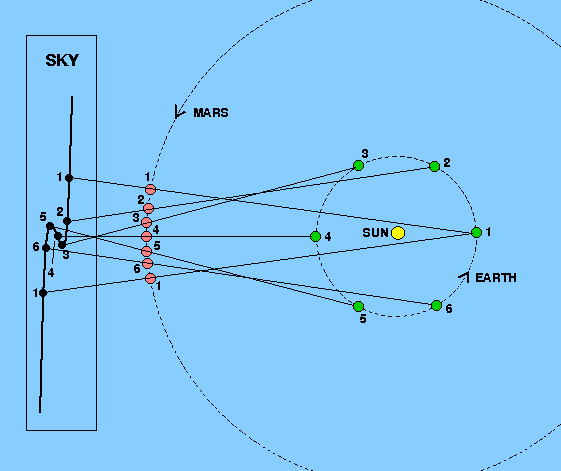
Copernicus also derived an important relationship between the synodic and sidereal periods of a planet in his heliocentric model. The synodic period, S, is the time it takes the planet to return to the same position in the sky relative to the Sun, as seen from the Earth. The sidereal period, P, is the time it takes the planet to complete one orbit of the Sun (i.e. it is the planet's orbital period). If the Earth's sidereal period is E, the Earth moves at the rate of 360°/E degrees per days in its orbit, while a planet's rate of angular motion is 360°/P as viewed from the Sun.

figure 29:

Successive similar configurations of two planets.

In Figure 29, the Earth moves from position 1 to position 2 after one orbit and then has S - E days to catch up with the superior planet at opposition again (at position 3). During this time, the superior planet has moved from position 1 to position 3. So the Earth must traverse the angle (S - E) x (360°/E) in the same time that the superior planet traverses the angle S x (360°/P). Hence,

(S - E)(360°/E) = S(360°/P)

or

1/S = 1/E - 1/P

For an inferior planet, the Earth is a superior planet, and so we interchange E and P to arrive at Copernicus' result.

1/S = 1/P - 1/E (inferior)
1/S = 1/E - 1/P (superior).

This is a very useful relationship because we know the length of the year on the Earth, E, and it is a simple matter to time how long it takes to see, for example, two successive oppositions of a (superior) planet, S. Copernicus' relation can then be used to determine the length of the year, P, on any planet in the solar system, as shown in the example problems.

Because the predictions of the Copernican model were no better than those of the Ptolemaic model, and because of the deep psychological and religious opposition to the move away from an Earth-centred Universe, the Copernican Universe was slow to be accepted. It was not until 1609, when Galileo built his first telescope and discovered, amongst other things, the moons of Jupiter (implying that not everthing revolves around the Earth) and all the phases of Venus (implying that Venus revolves around the Sun, not the Earth), that the Copernican model, or at least the heliocentric nature of our Solar System, was finally confirmed.