Kepler also investigated the speeds of the planets and found that the closer
in its orbit a planet is to the Sun, the faster it moves. Drawing a straight
line connecting the Sun and the planet (the radius vector), he
discovered that he could express this fact in his second law - the law of
areas:
For any planet the radius vector sweeps out equal areas in equal
times.
|
figure 32:
|
Kepler's second law.
|
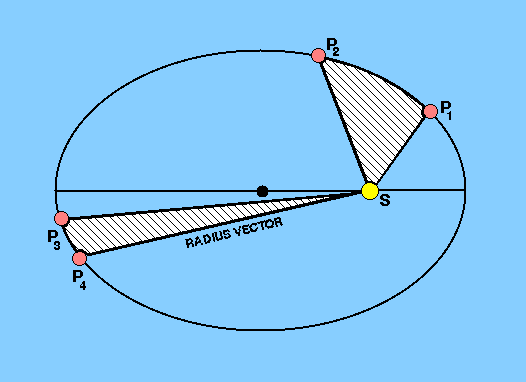
Figure 32 shows the positions of a planet,
P1, P2, P3,
P4, at times
t1, t2, t3,
t4. Between times t1 and
t2 the planet's radius vector sweeps out the area
bounded by the radius vectors SP1,
SP2 and the arc
P1P2. Similarly, the area
swept out by the radius vector in the time interval
(t4-t3) is the area
SP3P4. Then, Kepler's second
law states that:
area SP1P2 /
(t2-t1) =
area SP3P4 /
(t4-t3) = constant.
If t2-t1 =
t4-t3, then
area SP1P2 =
area SP3P4.
If the area is the area of the ellipse itself (which is given by
ab), the
radius vector will be back to its original position and Kepler's
second law therefore implies that the planet's orbital period is
constant.
It is possible to derive a mathematical expression for Kepler's
second law by supposing that the time interval
(t2-t1) is very small
and equal to interval (t4-t3).
Position P2 will be very close to
P1, just as P4 will be close
to P3. The area
SP1P2 is then approximately
the area of triangle SP1P2,
or
½SP1 x SP2 x
sin P1SP2.
If angle P1SP2 is expressed
in radians we may write
sin P1SP2 = angle
P1SP2 =
1,
since angle P1SP2 is very small.
Also,
SP1 = SP2 =
r1, say,
so that the area SP1P2 is given
by
½r211.
Similarly, area SP3P4 is given
by
½r222,
where SP3 = r2 and angle
P3SP4 =
2.
Let t4-t3 =
t2-t1 = t. Then, from
Kepler's second law,
½r21(1 / t) =
½r22(2 / t) = constant.
But /t is the
angular velocity, 
,
in the limit when t tends to zero. Hence
½r211 =
½r222
= constant,
is the mathematical expression of Kepler's second law. In order for this
law to be obeyed, the planet has to move fastest when its radius vector
is shortest, at perihelion, and slowest when it is at aphelion, as
shown in this java applet.
©Vik Dhillon, 30th September 2009
