free spectral range

The grating equation, n λ = d sin , tells us that light of wavelength λ in the first order is diffracted by exactly the same angle as light of wavelength λ/2 in the second order, as well as λ/3 in the third order, etc. In practice, this means that different spectral orders will overlap, as illustrated in figure 98.

figure 98:

Schematic showing the overlap between the first, second and third spectral orders produced by a diffraction grating. The wavelength range in each spectrum is limited by the CCD detector, which is only sensitive to light in the range ~3000-10,000 Å. The horizontal red lines mark the cut-point of the commonly-used GG495 order-sorting filter.

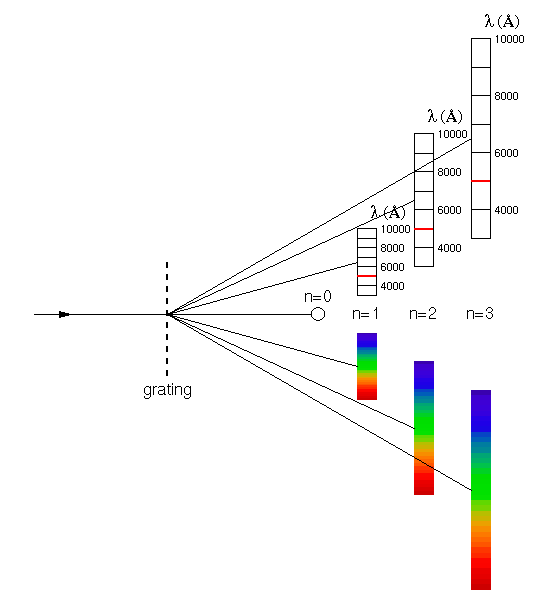
For example, figure 98 shows that light of wavelength 10,000 Å in the first order will fall on the same location on the detector as light of wavelength 5000 Å in the second order and 3333 Å in the third order, etc. The amount of overlap between the orders gets worse as the order number increases. Assuming that each order contains the same, fixed range of wavelengths, as depicted in figure 98, then the amount of spectrum in a given order that does not overlap with the next order up is known as the free spectral range. We can derive an expression for the free spectral range in a given order by noting that two wavelengths in adjacent orders, λ₁ and λ₂, that fall on top of each other must satisfy the relation n λ₁ = (n + 1) λ₂. Setting λ₂ as the minimum wavelength present in each order (e.g. 3000 Å in figure 98), then the free spectral range, FSR, is given by:

FSR = λ₁ - λ₂ = λ₂ / n.

Hence, for order n = 1 in figure 98, FSR = 3000 / 1 = 3000 Å, and for order n = 2, FSR = 3000 / 2 = 1500 Å.

order sorting

The first-order spectrum of an astronomical source will be contaminated by second-order light. If the grating being used is blazed to the first order, the contaminating second-order spectrum is likely to be very weak, but it can still be problematic if observing a blue object in the red end of the first order. For example, if one is interested in the spectral range 6000-10,000 Å in the first order, this region will be contaminated by light from 3000-5000 Å in the second order.

One way of eliminating the second-order contamination is to use an order-sorting filter. This is a filter which obscures all light below a certain wavelength and transmits everything above it. For example, a common order-sorting filter is GG495, which transmits all light above 4950 Å and blocks everything below it. This filter would be inserted in the collimated beam of the spectrograph, thus leaving the spectrograph focus unchanged, and will prevent all light below 4950 Å from hitting the grating (see figure 98). Since, in the above example, one is only interested in the range 6000-10,000 Å, this is not a problem, and it has the advantage that the contaminating second-order light between 3000-5000 Å is almost entirely eliminated.

The free spectral range is largest in the first order, making order-sorting relatively straightforward. This is the reason why spectrographs designed to work in the first order are so popular. However, if higher spectral resolution is required, it is much better to work in higher orders. In this case, the use of order-sorting filters is impractical, as the reduced free spectral range means that too much of the spectrum would have to be blocked. An alternative approach to order sorting is therefore required, a subject we shall turn to now.