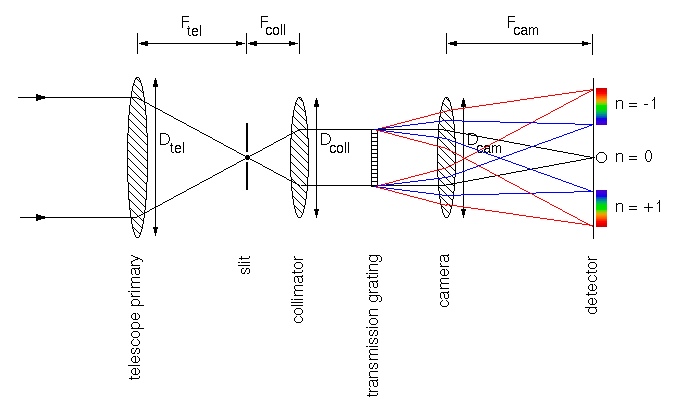
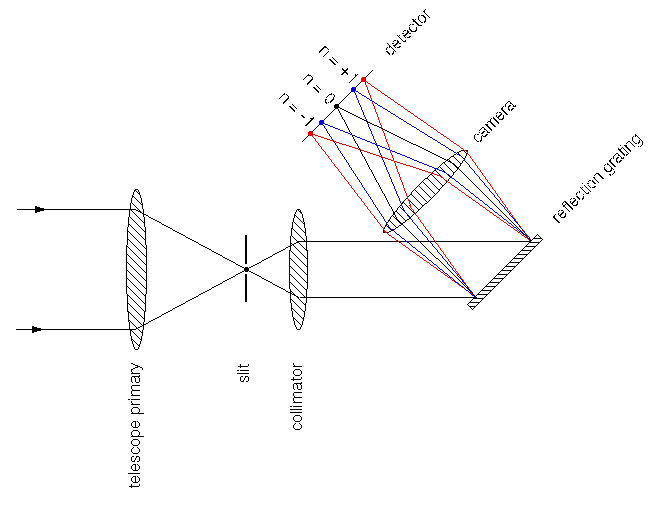
Most astronomical spectrographs have the same basic design, regardless of whether they are to be used for low-, medium- or high-resolution spectroscopy. A schematic is shown in figure 90.

figure 90:

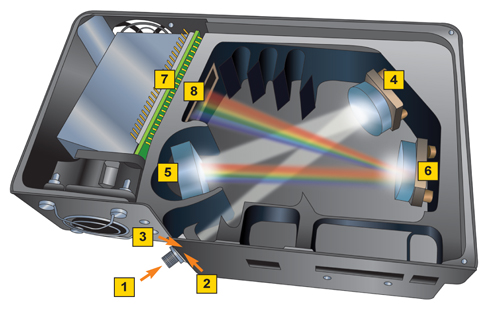
Top left: schematic of an astronomical spectrograph incorporating a transmission grating. The slit is in the focal plane of the telescope. The grating is conjugate with the primary mirror. The detector is in the focal plane of the camera. Top right: as above, but incorporating a reflection grating. Bottom: the light path through a commercial spectrograph, showing the principal components: the slit (2), collimator (4), reflection grating (5), camera (6) and detector (7).

 

The five basic components of an astronomical spectrograph are the slit, collimator, grating, camera and detector, each of which are described in more detail below. Note that, with the exception of the slit and grating, spectrographs have the same basic layout as re-imagers, and hence much of the material we covered on the latter topic will be applicable here.

slit

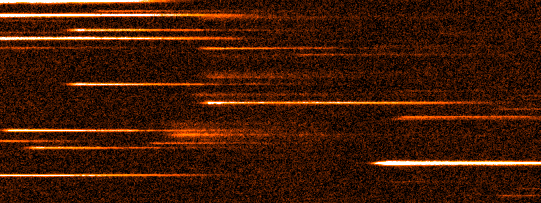
The slit is a mask with a narrow rectangular aperture that is placed in the focal plane of the telescope. The slit has two main functions. First, the slit acts as a means of isolating the region of interest on the sky; only light falling on the slit may enter the spectrograph, as shown in figure 91. Without a slit present, the spectra from sources either side of the target would overlap, contaminating the target spectrum. Additional sky background from either side of the target would also be recorded, degrading the signal-to-noise ratio of the spectrum.

figure 91:

Top left: Photograph of an adjustable slit. Top middle: image of a star field. Top right: the same star field, but imaged by a slitless spectrograph. Note how the spectra of objects at the same y position in the image overlap. Bottom: ULTRASPEC data showing the image of a star field recorded with the slit and grating removed from the beam (left), the image of the star field when just the slit is inserted into the beam (centre), and the spectra of the stars on the slit that result when the grating is also inserted into the beam (right). The y axis is the spatial direction and the x axis is the dispersion direction.

    

     

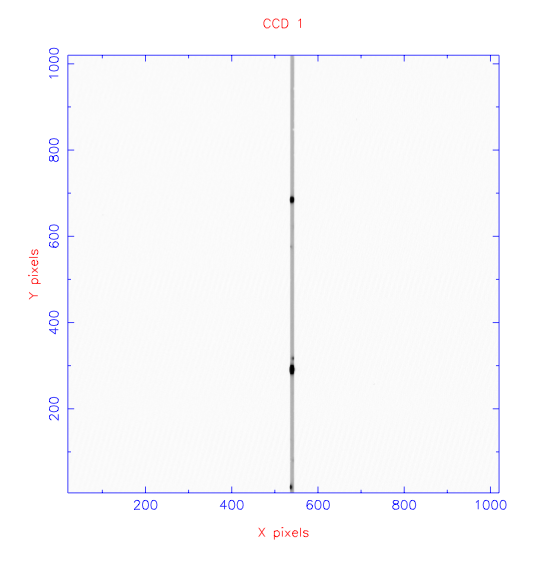
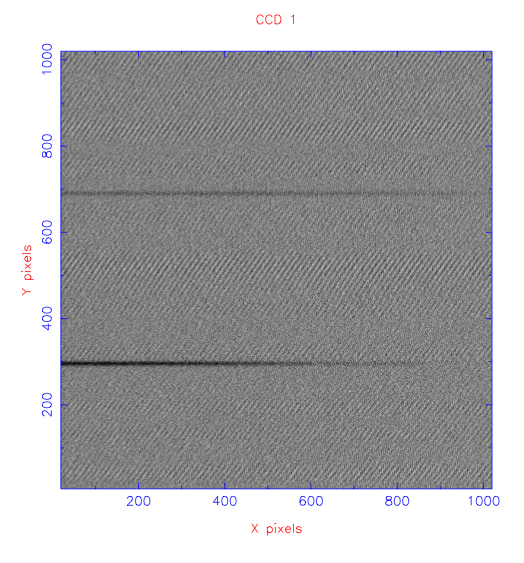
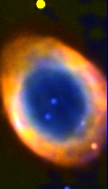
The second function of the slit is to provide stable spectral resolution. This can be understood by noting that a spectrum is essentially an infinite number of images of the telescope focal plane, each shifted slightly in wavelength. Hence, without a slit present, the spectral resolution of a star would be defined by the width of the star, i.e. the seeing. However, since seeing varies with time, the spectral resolution would then vary with time. The situation is even worse if a source is extended, such as the planetary nebula shown in the top panel of figure 92. In this case, individual spectral lines would appear as multiple images of the extended source, each shifted in wavelength, making detailed analysis of the lines almost impossible. The solution is to illuminate a narrow slit with the source, so that the spectrum becomes an infinite number of images of the slit, not the source. The minimum width of the spectral lines would then be defined by the slit width, as shown in the bottom panel of figure 92, and would hence be stable.

Spectrographs re-image, or project, the slit in the focal plane of the telescope onto the detector, which lies in the focal plane of the camera. As we discovered when looking at re-imagers, the ratio of the camera to collimator focal lengths determines the magnification of the image of the slit on the detector: M = F_cam / F_coll. Hence a slit of width 50 μm in a spectrograph with a collimator of focal length 500 mm and camera of focal length 250 mm would be projected to a width of 25 μm on the detector.

We shall discuss the issue of the optimum slit width to use when we look at spectral resolution.

figure 92:

Top: Image (left) and slitless spectrum (right) of the Ring Nebula (M57), showing that individual spectral lines take on the appearance of the nebula. Bottom left: Photograph of light illuminating five different slits of width, from top-to-bottom, 400 μm, 100 μm, 50 μm, 200 μm and 400 μm. Bottom middle: spectra of a hydrogen lamp, produced by illuminating the slits in the left-hand panel. Note how the spectrum is made up of images of the slit shifted in wavelength. Bottom right: spectra of the night sky emission lines, produced by illuminating the slits in the left-hand panel; the central spectrum also shows the spectrum of a star superimposed on the sky spectrum. Note how the width of the sky lines is set by the width of the slit.

  

     

collimator

The collimator in an astronomical spectrograph takes the diverging light from the slit, makes it parallel and directs the collimated beam towards the grating. Without a collimator, the diverging light from the slit would hit the grating, resulting in variable angles of incidence as a function of position on the grating. Inspecting the grating equation, it can be seen that varying the angle of incidence implies that the angle of diffraction must also vary for a fixed wavelength and spectral order. Hence the same wavelength of light in the same order would be imaged onto different positions on the detector, blurring the resulting spectrum. With a collimator, however, all angles of incidence on the grating are equal and no such blurring would result.

Collimators can be either lenses or mirrors and, as discussed in the section on re-imagers, the collimator must have the same focal ratio as the telescope and be positioned at a distance equal to its focal length from the telescope focal plane.

grating

The diffraction grating splits the light into its component wavelengths and can be of either the transmission or reflection variety, as shown in figure 90. The grating is usually positioned in the collimated beam so that it is conjugate with the primary mirror, which is advantageous as the minimum-sized (and hence cheapest) grating is then required to collect light from all angles incident on the primary mirror.

The grating equation shows that changing the angle of the grating with respect to the incident beam, , changes the angle of the diffracted beam, . Hence most spectrographs have gratings that can be tilted in order to adjust the start and end wavelengths of the spectrum.

camera

The role of the camera in an astronomical spectrograph is to collect the spectrally-dispersed beams from the grating, which are still collimated, and make them converge so that the spectrum is imaged onto the detector. The camera can be either a lens, mirror, or catadioptric system.

detector

The dispersed light is ultimately imaged by the spectrograph onto the detector, forming a spectrum, as shown in the bottom-right panel of figure 91. We can define the direction along the slit (i.e. the vertical direction in the bottom-right panel of figure 91) as the spatial axis, and the direction along the spectrum (i.e. the horizontal direction in the bottom-right panel of figure 91) as the dispersion axis.

Clearly, single pixel detectors are inappropriate for use in spectrographs, as the amount of light at each wavelength must be recorded. In principle, a detector composed of a one-dimensional array of pixels could be used to record a spectrum. However, such a detector would suffer from the same disadvantages that were listed for single-pixel detectors used for imaging, i.e. no spatially extended sources could be studied, no simultaneous sky background could be measured, and oversized pixels in the spatial direction would have to be used to collect all of the stellar flux, degrading the signal-to-noise ratio due to the additional sky background detected. For this reason, the detector of choice on virtually all of the world's astronomical spectrographs is two-dimensional - the CCD detector.