To perform calculations with planar triangles it is necessary to
use the formulae of planar trigonometry, which you will have met
before. Similarly, to perform calculations with
spherical triangles it
is necessary to use the formulae of
spherical trigonometry, which are given below.
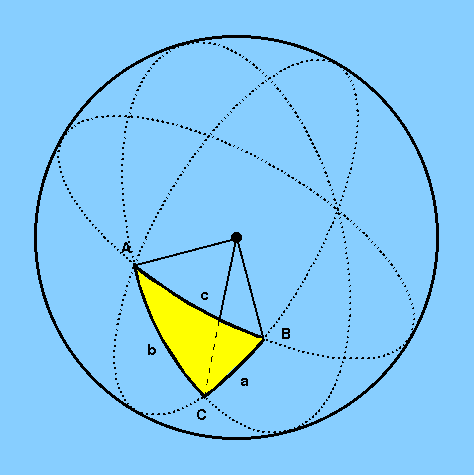
Figure 3 shows a spherical triangle, formed
by three intersecting great circles, with arcs of
length (a,b,c) and vertex angles of (A,B,C).
|
figure 3:
|
a spherical triangle with arcs of
length (a,b,c) and vertex angles of (A,B,C).
|
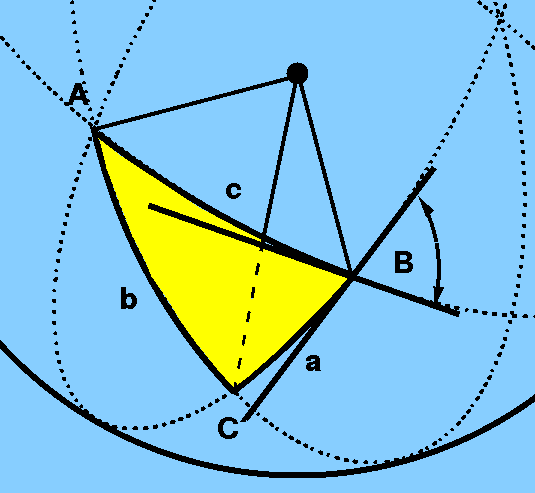
Note that the angle between two sides of a spherical triangle is
defined as the angle between the tangents to the two great
circle arcs, as shown in Figure 4 for vertex angle B.
|
figure 4:
|
the vertex angle B is defined as the angle between the
tangents to the two great circle arcs.
|
The arc lengths (a,b,c) and vertex angles (A,B,C) of
the spherical triangle in Figure 4 are related by the following formulae:
The sine formula:
(sin a / sin A) =
(sin b / sin B) =
(sin c / sin C)
The cosine formula:
cos a = cos b cos c + sin b sin c cos A
These are the spherical analogues of the cosine and sine
formulae of planar trigonometry. Their proofs are given
on pages 52-54 of Roy and Clarke, along with a host of other
formulae which you will not need to know - almost all of
the simple problems you will encounter in spherical astronomy
can be solved using just the sine and/or cosine formulae given
above. The trick is to know which triangle to draw - once you
have done this, the solution is easy, as shown in the
example problems.
©Vik Dhillon, 30th September 2009

